2019CCF非专业级别软件能力认证第一轮试卷
入门级C++语言试题A卷
认证时间:2019年10月19日
一、单项选择题(共15题,每题2分,共计30分;每题有且仅有一个正确选项)
1.中国的国家顶级域名是()
A. .cn
B. .ch
C. .chn
D. .china
答案:A
解析:常识,中国国家顶级域名即是.cn
2.二进制数 11 1011 1001 0111 和 01 0110 1110 1011 进行逻辑与运算的结果是()
A.01 0010 1000 1011
B.01 0010 1001 0011
C.01 0010 1000 0001
D.01 0010 1000 0011
答案:D
解析:逻辑“与”基本常识,当且仅当2个数对应位都为1时,答案该位为1
3.32位整型变量占用()个字节。
A.32
B.128
C.4
D.8
答案:C
解析:一个字节是8位,因此32位对应4个字节
4.若有如下程序段,其中s、a、b、c均已定义为整型 变量,且a、c均已赋值(c大于0)
s = a; for (b = 1; b <= c; b++) s= s -1; 则与上述程序段功能等价的赋值语句是()
A. s=a-c;
B. s=a-b;
C. s=s-c;
D. s=b-c;
答案:A
解析:s 初始化为a; for循环执行c次,每次s减1,共减 c,所以s=a-c
5.设有100个已排好序的数据元素,采用折半查找时,最大比较次数为()
A.7 B.10 C.6 D.8
答案:A
解析:对折半查找,第一次(1+100)/2 = 50,第二次(1+50)/2 = 25, 第三次(1+25)/2 = 13, 第四次(1+13)/2 = 7, 第五次(1+7)/2= 4, 第六次(1+4)/2 = 2, 第七次(1+2)/2 = 1。
6.链表不具有的特点是()
A.插入删除不需要移动元素
B.不必事先估计存储空间
C.所需空间与线性表长度成正比
D.可随机访问任一元素
答案:D
解析:链表没有下标,不可随机访问
7.把8个同样的球放在5个同样的袋子里,允许有的袋子空着不放,问共有多少种不同的分法?()提示:如果8个球都放在一个袋子里,无论是哪个袋子,都只算同一种分法
A .22
B .24
C .18
D .20
答案:C
解析:整数拆分问题,8拆成至多5个数之和(不计顺序),可按袋子个数分类讨论:1个袋子1种,2个袋子4种,3个袋子5种,4个袋子5种,5个袋子3种,共18种
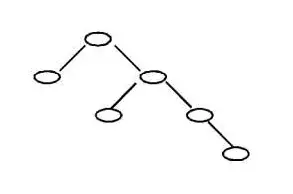
8.—棵二叉树如右图所示,若采用顺序存储结构,即用一维数组元素存储该二叉树中的结点(根结点的下标为1,若某结点的下标为i ,则其左孩子位于下标2i 处、右孩子位于下标2i +1处),则该数组的最大下标至少为()。
A .6 B .10 C .15 D .12
答案:C
解析:堆式编号,最大值是最深的那层最靠右侧的节点,编号为((1*2+1)*2+1)*2+1=15
9.100以内最大的素数是()
A .89 B . 97 C .91 D .93
答案:B
解析:91 = 7*13, 93 = 3 * 31, 97 > 89, 且为素数.
10.319 和 377的最大公约数是()
A .27 B .33 C .29 D .31
答案:C
解析:辗转相除法,最大公约数为:(319,377)=(319,58)=(58,29)=29
11.新学期开学了,小胖想减肥,健身教练给小胖制定了两个训练方案。方案一每次连续跑3公里可以消耗300千卡(耗时半小时);方案二每次连续跑5公里可以消耗600干卡(耗时1小时)。小胖每周周一到周四能抽出半小时跑步,周五到周日能抽出一小时跑步。另外,教练建议小胖每周最多跑21公里,否则会损伤膝盖。请问如果小胖想严格执行教练的训练方案,并且不想损伤膝盖,每周最多通过跑步消耗多少千卡?()
A .3000 B .2500 C .2400 D .2520
答案:C
解析:设方案1,2各i, j天,由题意,3i +5j <=21,i +j <=7,j <=3. 求300i+600j的最大值。枚举所有情况,当i =2, j =3时,最大值2400,或使用线性规划求解。
12.一副纸牌除掉大小王有52张牌,四种花色,每种花色13张。假设从这52张牌中随机抽取13张纸牌,则至少()张牌的花色一致。
A .4 B .2 C .3 D .5
答案:A
解析:抽屉原理,13张牌最坏情况就是4种花色分別为3,3,3,4张,至少4张一个样花色。
13.—些数字可以颠倒过来看,例如0、1、8颠倒过来还是本身,6颠倒过来是9, 9颠倒过来看还6,其他数字颠倒过来都不构成数字。类似的,一些多位数也可以颠倒过来看,比如106颠倒过来是901。假设某个城市的车牌只由5位数字组成,每一位都可以取0到9。请问这个城市最多有多少个车牌倒过来怡好还是原来的车牌?()
A .60 B .125 C .75 D .100
答案:C
解析:前俩位位有5种选法(0,1,6,8,9),第3位有3种(0,1,8),第4, 5位由前2位决定,答案为55311=75
14.假设一棵二叉树的后序遍历序列为DGJHEBIFCA,中序遍历序列为DBGEHJACIF,则其前序遍历序列为()。
A.ABCDEFGHIJ
B.ABDEGHJCFI
C.ABDEGJHCFI
D.ABDEGHJFIC
答案:B
解析:后续遍历是“左右根”,中序遍历是“左根右”,后序最后的A是根,中序中看的 DBGEH是左子树,右边的CIF是右子树,以此类推可求画出树的形态,再求前序
15.以下哪个奖项是计算机科学领域的最高奖?()
A.图灵奖 B.鲁班奖 C.诺贝尔奖 D.普利策奖
答案:A
解析:鲁班奖是国内建设工程;诺贝尔奖为物理、化学、医学、文学、和平;普利策奖是新闻奖,图灵奖由美国计算机协会(ACM)于1966年设立,专门奖励那些对计算机事业作出重要贡献的个人。
二、阅读程序(程序输入不超过数组或字符串定义的范围;判断题正确填✓,错误填✗;除特殊说明外,判断题1.5分,选择题4分,共计40分)
|
|
概述:将字符串下标是n约数位置的小写字母转大写
•判断题
1)输入的字符串只能由小写字母或大写字母组成。()
答案:错
解析:输入的字符串也可以包含数字等其它字符。
- 若将第8行的“i=1”改为“i =0”,程序运行时会发生错误 。( )
答案:对
解析:除数不能为0,%0会发生错误。
- 若将第8行的“i<=n”改为“i*i<=n”,程序运行结果不会改变。()
答案:错
解析:循环条件为<=n, 也 就 是n也会执行到。同时 n%n==0恒为True,所以修改后少了n这次循环,也就会改变结果了
- 若输入的字符串全部由大写字母组成,那么输出的字符串就跟输入的字符串一样。()
答案:对
解析:对的,因为大写的ASCII值比较小,也就是从c>=a恒为False,所以s的值不会改变,所以是对的
•选择题
- 若输入的字符串长度为18,那么输入的字符串跟输出的字符串相比,至多有()个字符不同。
A.18
B.6
C.10
D.1
答案:B
解析:因为$$ 18=2\times3^2$$, 也 就 是 因 数 个 数 为$$(1+1)\times(1+2)=6$$ ,也就是判定条件最多满足六次,所以最多有6 个。
- 若输入的字符串长度为(),那么,输入的字符串跟输出的字符串相比,至多有36个字符不同。
A.36
B.100000
C.1
D.128
答案:B
解析:因为$$100000=2^5\times5^5$$ ,也就是因数个数为 $$(5+1)\times(5+1)=36$$,也即是判定条件最多满足36次,所以最多有36个。
|
|
假设输入的n和m都是正整数,x和y都是在[1,n]的范围内的整数,完成下面的判断题和选择题
判断题:
1)当m>0时,输出的值一定小于2n。
答案:对
解析:由限定条件可知,0<x,y<= n, 当m大于0时,一定存在某个数被选中,使得 ans<2*n。
2)执行完第27行的“++ans”时,ans一定是偶数。
答案:错
解析:由于数对是一个左值与一个右值相匹配,所以ans最终一定是偶数,但是第27行的”++ans“在23行循环内部,其中间结果可能是负数。
- a[i]和b[i]不可能同时大于0。
答案:错
解析:反例:当m为1,并且输入x=1,y=1的时候,可以使得a[1]和b[1]同时为1
- 若程序运行到第13行时,x总是小于y,那么第15行不会被执行。
答案:错
解析:反例m=2, x=1,y=2.x=1,y=3
选择题
- 若m个x‘两两不同,且m个y两两不同,则输出的值为()
A.2n-2m
B.2n+2
C.2n-2
D.2n
答案:A
解析:如果各不相同的话,m次循环,会导致2m个位置从0变到整数,答案为2n-2m
6)若m个x两两不同,且m个y都相等,则输出的值为()
A.2n-2
B.2n
C.2m
D. 2n-2m
答案:A
解析:都不相同的话14行和16行不会执行,因此每次输入会有一组a,b赋值一共有m组;y都相同的话b[y]中会 保留最小的一个x,所以只存了一组值,空着2n-2
|
|
概述:构造数列a的笛卡尔树(根节点最小且保持中序遍历),并求节点深度与b的加权和
判断题
- 如果a数组有重复的数字,则程序运行时会发生错误。()
答案:错
解析:每次找a数组中第一次出现的最小值,所以有重 复的数不会导致程序出错
- 如果b数担全为0,则输出为0()
答案:对
解析:因为递归最底层l>r返回0,而倒数第二层返回值是O+0+depth*b[mink],如果b是0的话也是0,以此类推,返回结果总是0
选择题
- 当n=100时,最坏情况下,与第12行的比较运算执行的次数最接近的是()
A.5000
B.600
C.6
D.100
答案:A
解析:最坏情况下a有序,mink每次都切在一段,递归 进行100层,执行次数为100+99+, +…1约等于5000
- 当n=100时,最好情况下,与第12行的比较运算执行 的次数最接近的是()
A.100
B.6
C.5000
D.600
答案:D
解析:最好情况下,每次都均分,每层递归总次数为 100,层数为logn约等于6,总次数月6*100=600
5)当n=10时,若b组满足,对任意Osi<n,都有b[i]=i +1,那么输出最大为()
A.386
B.383
C.384
D.385
答案:D
解析:n=10时,深度最大能够达到10,最大输出为 1b[0]+2b[1]+…+10b[9]=11+22+33+44+55+66+77+88+99+10*10=385
6)(4分)当n=100时,若b数组满足,对任意0<=i<n,都 有b[i]=1,那么输出最小为()
A.582
B.580
C.579
D.581
答案:B
解析:b=1,即求一个100节点的二叉树,节点深度之 和最小,贪心法,结论是100节点的完全二叉树。11+22+43+84+165+326+37*7=580
三、完善程序(单选题,每题3分,共计30分)
1.(矩阵变幻)有一个奇幻的矩阵,在不停的变幻,其变幻方式为:数字0变成矩阵$\begin{bmatrix} 0&0 \\ 0&1 \end{bmatrix}$$,数字1变成矩阵$$\begin{bmatrix} 1&1 \\ 1&0 \end{bmatrix}$。最初该矩阵只有一个元素0,变幻n次后,矩阵会变成什么样? 例如,矩阵最初为: [0]; 矩阵变幻1次后:$\begin{bmatrix}0&0 \\ 0&1\end{bmatrix}$;矩阵变幻2次后:$\begin{bmatrix}0&0&0&0 \\ 0&1&0&1 \\ 0&0&1&1 \\ 0&1&1&0 \end{bmatrix}$。 输入一行一个不超过10的正整数n。输出变幻n次后的矩阵。 试补全程序。 提示: “«”表示二进制左移运算符,例如(11)2«2= (1100)2; 而“^”表示二进制异或运算符,它将两个参与运算的数中的每个对应的二进制位一一 进行比较,若两个二进制位相同,则运算结果的对应二进制位为0,反之为1。
1)①处应填()
A. n%2
B.0
C.t
D.1
答案:C
解析:递归边界,res只有这一处赋值,BD显然错。n%2的话01只跟n有关,错,因此只有t是对的
2)②处应填()
A.x - step,y- step
B.x,y-step
C.x-step.y
D.x,y-step
答案:D
解析:step是边长的一半,借鉴15, 16行,参数x,y是 当前左上角坐标。14-17
分别是左上,左下,右上,右 下四个子矩阵
3)③处应填()
A.x-step, y-step
B.x+step,y+step
C.x-step, y
D.x, y-step
答案:B
解析:同上
- ④处应填()
A.n-1, n % 2
B.n,0
C.n, n % 2
D.n-1,0
答案:B
解析:此处是递归计算的入口,即题目最终所求的大小为$$2^n\times2^n$$,由单个数字 0 变化来的矩阵,因此递归函数的另俩个参数为 n, 0
- ⑤处应填()
A. 1«(n+1)
B.1«n
B. n+1
D.1«(n-1)
答案:B
解析:size是输出矩阵的边长,也就是2^n,用位运算 写就是1«n
2.(计数排序)计数棑序是一个广泛使用的排序方法.下而的程序使用双关键字计数排序,将n对10000以内的整数,从小到大排序。
例如有三对整数(3,4)、(2,4)、(3,3),那么排序之后应该是(2,4)、(3,3)、(3,4).输入第一行为n,接下来n行,第i行有两个数a[i]和b[i],分別表示第 i对整数的第一关键字和第二关键字。从小到大排序后输出。
数据范围:
提示:应先对第二关键字排序,再对第一关键字排序。数组ord[]存储第二关键字排序的结果,数组rest[]存储双关键字样序的结果,试补全程序。
|
|
1)①处应填()
A. ++cnt[i]
B. ++cnt[b[i]]
C. ++cnt[a[i] * maxs + b[i]]
D. ++cnt[a[i]]
答案:B
解析:此处是对第二关键字进行计数排序。题目中给出提示,先按第二关键字排序。并且根据填空2对ord进行更改, 可知此时是対第二关键字进行排序。
2)②处应填()
A. ord[–cnt[a[i]]]=i
B. ord[–cnt[b[i]]]=a[i]
C. ord[–cnt[a[i]]]=b[i]
D. ord[–cnt[b[i]]]=i
答案:D
解析:cnt[b[i]]表示按第二关键字,第i个数排第几位。ord[i]表示第i小的数在原序列的位置
3)③处应填()
A. ++cnt[b[i]]
B. ++cnt[a[i] * maxs + b[i]]
C. ++cnt[a[i]]
D. ++cnt[i]
答案:C
解析:对第一关键字计数,并做各关键词的数量统计工作,因此将a[i]对应的元素数量自增一。
4)④处应填()
A. res[-cnt[a[ord[i]]]]=ord[i]
B. res[-cnt[b[ord[i]]]]=ord[i]
C. res[-cnt[b[i]]]=ord[i]
D. res[-cnt[a[i]]]=ord[i]
答案:A
解析:对应填空2 ord[i]记录了第二关键字第i小 的数在原序列的位置。此时res[i]记录了第一关键字第i小的数在原序列的位置。
5)⑤处应填()
A. a[i],b[i]
B.a[res[i]],b[res[i]]
C.a[ord[res[i]]],b[ord[res[i]]]
D.a[res[ord[i]]],b[res[ord[i]]]
答案:B
解析:此处是按顺序输出排序结果,由于之前已经按照第二、第一关键字进行计数排序,所以此时第i 个元素的原始下标为 res[i].
- 原文作者:图图爸爸
- 原文链接:https://www.tubacode.com/post/csp-j-first-2019.html
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。