提高级C++语言试题
认证时间:2021年9月19日 09:30~11:30
一、单项选择题(共 15 题,每题 2 分,共计 30 分;每题有且仅有一个正确选项)
1、在 Linux 系统终端中,用于列出当前目录下所含的文件和子目录的命令为( )。
A. ls
B. cd
C. cp
D. all
【参考答案】A
2、二进制数 $00101010_2 $和 $00010110 _2$ 的和为( )。
A. $00111100_2$
B. $01000000_2$
C. $00111100_2$
D. $01000010_2$
【参考答案】B
3、在程序运行过程中,如果递归调用的层数过多,可能会由于( )引发错误。
A. 系统分配的栈空间溢出
B. 系统分配的队列空间溢出
C. 系统分配的链表空间溢出
D. 系统分配的堆空间溢出
【参考答案】A
4、以下排序方法中,( )是不稳定的。
A. 插入排序
B. 冒泡排序
C. 堆排序
D. 归并排序
【参考答案】C
5、以比较为基本运算,对于 $2n$ 个数,同时找到最大值和最小值,最坏情况下需要的最小的比
较次数为( )。
A. $4n-2$
B. $3n+1$
C. $3n-2$
D. $2n+1$
【参考答案】C
6、现有一个地址区间为 $0~10$ 的哈希表,对于出现冲突情况,会往后找第一个空的地址存储
(到 10 冲突了就从 0 开始往后),现在要依次存储$(0,1, 2,3,4,5,6,7)$,哈希函
数为 $h(x)=x^2 mod 11$。请问 $7$ 存储在哈希表哪个地址中( )。
A. 5
B. 6
C. 7
D. 8
【参考答案】C
7、G 是一个非连通简单无向图(没有自环和重边),共有 $36$ 条边,则该图至少有( )个点。
A. 8
B. 9
C. 10
D. 11
【参考答案】C
8、令根结点的高度为 1,则一棵含有 2021 个结点的二叉树的高度至少为( )。
A. 10
B. 11
C. 12
D. 2021
【参考答案】B
9、前序遍历和中序遍历相同的二叉树为且仅为( )。
A. 只有 1 个点的二叉树
B. 根结点没有左子树的二叉树
C. 非叶子结点只有左子树的二叉树
D. 非叶子结点只有右子树的二叉树
【参考答案】D
10、定义一种字符串操作为交换相邻两个字符。将“DACFEB”变为 “ABCDEF”最少需要( )
次上述操作。
A. 7
B. 8
C. 9
D. 6
【参考答案】A
11、有如下递归代码
solve(t, n):
if t=1 return 1;
else return 5*solve(t-1,n) mod n;
则 solve(23,23)的结果为( )。
A. 1
B. 7
C. 12
D. 22
【参考答案】A
12、斐波那契数列的定义为:$F_1 =1,F_2 =1,F_n =F_{n-1}+F_{n-2} \quad (n>=3)$。现在用如下程序来计算斐波
那契数列的第 $n$ 项,其时间复杂度为( )。
F(n):
if n<=2 return 1;
else return F(n-1) + F(n-2);
A. $O(𝑛)$
B. $O(𝑛 ! )$
C. $O(2^n )$
D. $O(𝑛log𝑛)$
【参考答案】C
13、有 8 个苹果从左到右排成一排,你要从中挑选至少一个苹果,并且不能同时挑选相邻的两
个苹果,一共有( )种方案。
A. 36
B. 48
C. 54
D. 64
【参考答案】C
14、设一个三位数 $n= 𝑎𝑏𝑐$,$a, b, c$ 均为 $1~9$ 之间的整数,若以 $a, b, c$ 作为三角形的三
条边可以构成等腰三角形(包括等边),则这样的 $n$ 有( )个。
A. 81
B. 120
C. 165
D. 216
【参考答案】C
15、有如下的有向图,节点为 A, B, … , J, 其中每条边的长度都标在图中。则节点 A 到节
点 J 的最短路径长度为( )。
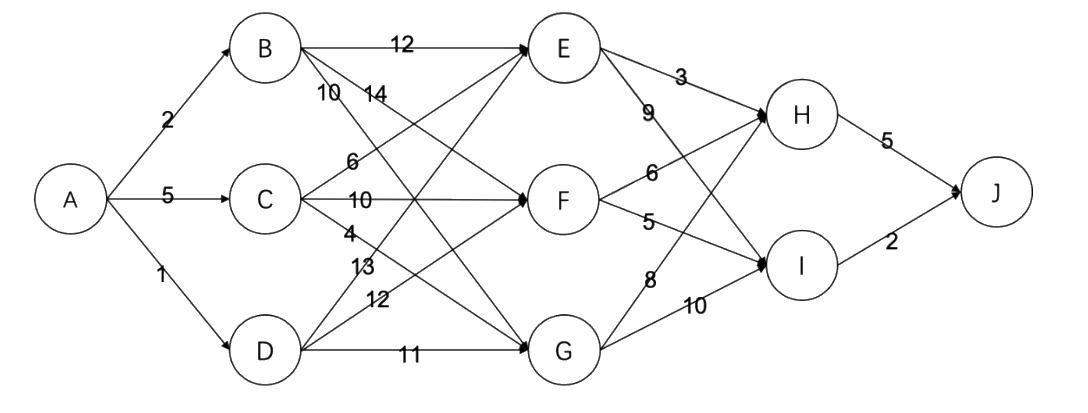
A. 16
B. 19
C. 20
D. 22
【参考答案】B
二、阅 读 程序(程序 输 入不 超 过数 组 或字符串定义的 范围 ; 判断 题正确 填 √ ,错误 填 × ; 除特殊说明外 , 判断 题 1.5 分,选择题 3 分,共计 40 分)
(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
#include <iostream>
#include <cmath>
using namespace std;
const double r = acos(0.5);
int a1, b1, c1, d1;
int a2, b2, c2, d2;
inline int sq(const int x) { return x * x; }
inline int cu(const int x) { return x * x * x; }
int main()
{
cout.flags(ios::fixed);
cout.precision(4);
cin >> a1 >> b1 >> c1 >> d1;
cin >> a2 >> b2 >> c2 >> d2;
int t = sq(a1 - a2) + sq(b1 - b2) + sq(c1 - c2);
if (t <= sq(d2 - d1)) cout << cu(min(d1, d2)) * r * 4;
else if (t >= sq(d2 + d1)) cout << 0;
else {
double x = d1 - (sq(d1) - sq(d2) + t) / sqrt(t) / 2;
double y = d2 - (sq(d2) - sq(d1) + t) / sqrt(t) / 2;
cout << (x * x * (3 * d1 - x) + y * y * (3 * d2 - y)) * r;
}
cout << endl;
return 0;
}
|
假 设 输 入的所有数的 绝 对值 都 不 超 过 1000 , 完成下面的判断 题和单选题 :
16、将第 21 行中 t 的类型声明从 int 改为 double, 不会 影响程序运行的结果。(√ )
17、将第 26、27 行中的“/ sqrt(t) / 2”替换为“/ 2 / sqrt(t)”, 不会 影响程序运行的结果。( ×)
18、将第 28 行中的“x * x”改成“sq(x)”、“y * y”改成“sq(y)” , 不会 影响程序运行的结果。(× )
19、( 2 分) 当输入为“0 0 0 1 1 0 0 1”时,输出为“1.3090”。(√ )
20、当输入为“1 1 1 1 1 1 1 2”时,输出为( )。
A. “3.1416” B. “6.2832” C. “4.7124” D. “4.1888”
【参考答案】D
21、( 2.5 分) 这段代码的含义为( )。
A. 求圆的面积并
B. 求球的体积并
C. 求球的体积交
D. 求椭球的体积并
【参考答案】C
(2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
#include <algorithm>
#include <iostream>
using namespace std;
int n, a[1005];
struct Node
{
int h, j, m, w;
Node(const int _h, const int _j, const int _m, const int _w):
h(_h), j(_j), m(_m), w(_w)
{ }
Node operator+(const Node &o) const
{
return Node(
max(h, w + o.h),
max(max(j, o.j), m + o.h),
max(m + o.w, o.m),
w + o.w);
}
};
Node solve1(int h, int m)
{
if (h > m)
return Node(-1, -1, -1, -1);
if (h == m)
return Node(max(a[h], 0), max(a[h], 0), max(a[h], 0), a[h]);
int j = (h + m) >> 1;
return solve1(h, j) + solve1(j + 1, m);
}
int solve2(int h, int m)
{
if (h > m)
return -1;
if (h == m)
return max(a[h], 0);
int j = (h + m) >> 1;
int wh = 0, wm = 0;
int wht = 0, wmt = 0;
for (int i = j; i >= h; i--) {
wht += a[i];
wh = max(wh, wht);
}
for (int i = j + 1; i <= m; i++) {
wmt += a[i];
wm = max(wm, wmt);
}
return max(max(solve2(h, j), solve2(j + 1, m)), wh + wm);
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
cout << solve1(1, n).j << endl;
cout << solve2(1, n) << endl;
return 0;
}
|
假设输入的所有数的绝对值都不超过1000 ,完成下面的判断题和单选题:
22、程序总是会正常执行并输出两行两个相等的数。(√)
23、第 28 行与第 38 行分别有可能执行两次及以上。(×)
24、当输入为“$5\quad -10 \quad 11 \quad -9 \quad 5 \quad -7$”时,输出的第二行为“$7$”。(×)
25、solve1(1, n) 的时间复杂度为( )。
A. $O(log𝑛)$
B. $O(𝑛)$
C. $O(𝑛log𝑛)$
D. $O(𝑛 !)$
【参考答案】B
26、solve2(1, n) 的时间复杂度为( )。
A. $O(log𝑛)$
B. $O(𝑛)$
C. $O(𝑛log𝑛)$
D. $O(𝑛 !)$
【参考答案】C
27、当输入为“$10\quad -3\quad 2\quad 10\quad 0\quad -8\quad 9\quad -4\quad -5\quad 9\quad 4$”时,输出的第一行为( )。
A. “13”
B. “17”
C. “24”
D. “12”
【参考答案】B
(3)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
|
#include <iostream>
#include <string>
using namespace std;
char base[64];
char table[256];
void init()
{
for (int i = 0; i < 26; i++) base[i] = 'A' + i;
for (int i = 0; i < 26; i++) base[26 + i] = 'a' + i;
for (int i = 0; i < 10; i++) base[52 + i] = '0' + i;
base[62] = '+', base[63] = '/';
for (int i = 0; i < 256; i++) table[i] = 0xff;
for (int i = 0; i < 64; i++) table[base[i]] = i;
table['='] = 0;
}
string encode(string str)
{
string ret;
int i;
for (i = 0; i + 3 <= str.size(); i += 3) {
ret += base[str[i] >> 2];
ret += base[(str[i] & 0x03) << 4 | str[i + 1] >> 4];
ret += base[(str[i + 1] & 0x0f) << 2 | str[i + 2] >> 6];
ret += base[str[i + 2] & 0x3f];
}
if (i < str.size()) {
ret += base[str[i] >> 2];
if (i + 1 == str.size()) {
ret += base[(str[i] & 0x03) << 4];
ret += "==";
}
else {
ret += base[(str[i] & 0x03) << 4 | str[i + 1] >> 4];
ret += base[(str[i + 1] & 0x0f) << 2];
ret += "=";
}
}
return ret;
}
string decode(string str)
{
string ret;
int i;
for (i = 0; i < str.size(); i += 4) {
ret += table[str[i]] << 2 | table[str[i + 1]] >> 4;
if (str[i + 2] != '=')
ret += (table[str[i + 1]] & 0x0f) << 4 | table[str[i + 2]] >> 2;
if (str[i + 3] != '=')
ret += table[str[i + 2]] << 6 | table[str[i + 3]];
}
return ret;
}
int main()
{
init();
cout << int(table[0]) << endl;
int opt;
string str;
cin >> opt >> str;
cout << (opt ? decode(str) : encode(str)) << endl;
return 0;
}
|
假设输入总是合法的(一个整数和一个不含空白字符的字符串,用空格隔开),完成下面的判断题和单选题:
28、程序总是先输出 一行 一个整数,再输出 一行 一个字符串。(×)
29、对于任意不含空白字符的字符串 str1,先执行程序输入“0 str1”,得到输出的第二行记为 str2;再执行程序输入“1 str2”,输出的第二行必为 str1。(√ )
30、当输入为“1 SGVsbG93b3JsZA==”时,输出的第二行为“HelloWorld”。(×)
31、设输入字符串长度为 $n$,encode 函数的时间复杂度为( )。
A. $O(\sqrt n)$
B. $O(n)$
C. $O(nlog n)$
D. $O(n!)$
【参考答案】B
32、输出的第一行为( )。
A. “0xff”
B. “255”
C. “0xFF”
D. “-1”
【参考答案】D
33、( 4 分) 当输入为“$0; CSP2021csp$”时,输出的第二行为( )。
A. “Q1NQMjAyMWNzcAv=”
B. “Q1NQMjAyMGNzcA==”
C. “Q1NQMjAyMGNzcAv=”
D. “Q1NQMjAyMWNzcA==”
【参考答案】D
三 、 完善 程序( 单选题,每小题 3 分,共计 30 分 )
(1) (魔 法数字)小 H 的魔法数字是 4。给定 𝑛,他希望用若干个 4 进行若干次加法、减法和整除运算得到 𝑛。但由于小 H 计算能力有限,计算过程中只能出现不超过𝑀 = 10000 的正整数。求至少可能用到多少个 4。
例如,当 𝑛 = 2 时,有 2 = (4 + 4)/4,用到了 3 个 4,是最优方案。
试补全程序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
#include <iostream>
#include <cstdlib>
#include <climits>
using namespace std;
const int M = 10000;
bool Vis[M + 1];
int F[M + 1];
void update(int &x, int y) {
if (y < x)
x = y;
}
int main() {
int n;
cin >> n;
for (int i = 0; i <= M; i++)
F[i] = INT_MAX;
①;
int r = 0;
while (②) {
r++;
int x = 0;
for (int i = 1; i <= M; i++)
if (③)
x = i;
Vis[x] = 1;
for (int i = 1; i <= M; i++)
if (④) {
int t = F[i] + F[x];
if (i + x <= M)
update(F[i + x], t);
if (i != x)
update(F[abs(i - x)], t);
if (i % x == 0)
update(F[i / x], t);
if (x % i == 0)
update(F[x / i], t);
}
}
cout << F[n] << endl;
return 0;
}
|
34、①处应填( )
A. F[4] = 0
B. F[1] = 4
C. F[1] = 2
D. F[4] = 1
【参考答案】D
35、②处应填( )
A. !Vis[n]
B. r < n
C. F[M] == INT_MAX
D. F[n] == INT_MAX
【参考答案】A
36、③处应填( )
A. F[i] == r
B. !Vis[i] && F[i] == r
C. F[i] < F[x]
D. !Vis[i] && F[i] < F[x]
【参考答案】D
37、④处应填( )
A. F[i] < F[x]
B. F[i] <= r
C. Vis[i]
D. i <= x
【参考答案】C
(2) ( RMQ 区间最值问题) 给定序列 $𝑎_0,\dots , 𝑎_{n-1}$,和 $𝑚$ 次询问,每次询问给定 $𝑙$,$𝑟$,求$max{𝑎_l,\dots ,𝑎_r}$ 。
为了 解决 该问题,有一个算法叫 the Method of Four Russians ,其 时间复杂度 为$𝑶(𝒏 + 𝒎)$ , 步骤如下:
- 建立 Cartesian(笛卡尔)树,将问题转化为树上的 LCA(最近公共祖先)问题。
- 对于 LCA 问题,可以考虑其 Euler 序(即按照 DFS 过程,经过所有点,环游回根的序列),即求 Euler 序列上两点间 一个 新 的 RMQ 问题。
- 注意新的问题为 ±1 RMQ,即相邻两点的深度差一定为 1。
下面解决这个 $±1$ RMQ 问题,“序列”指 Euler 序列:
- 设$t$为 Euler 序列长度。取 $b=[\frac{log_2 t}{2}]$。将序列每 $b$ 个分为一大块,使用 ST表(倍增表)处理大块间的 RMQ 问题,复杂度 $O(\frac{t}{b}logt)=O(n)$。
- (重点) 对于一个块内的 RMQ 问题,也需要$O(1)$ 的算法。由于差分数组 $2^{b-1}$种,可以预处理出所有情况下的最值位置,预处理复杂度 $O(b2^b)$,不超过$O(n)$。
- 最终,对于一个查询,可以转化为中间整的大块的 RMQ 问题,以及两端块内的 RMQ问题。
试补全程序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
|
#include <iostream>
#include <cmath>
using namespace std;
const int MAXN = 100000, MAXT = MAXN << 1;
const int MAXL = 18, MAXB = 9, MAXC = MAXT / MAXB;
struct node {
int val;
int dep, dfn, end;
node *son[2]; // son[0], son[1] 分别表示左右儿子
} T[MAXN];
int n, t, b, c, Log2[MAXC + 1];
int Pos[(1 << (MAXB - 1)) + 5], Dif[MAXC + 1];
node *root, *A[MAXT], *Min[MAXL][MAXC];
void build() { // 建立 Cartesian 树
static node *S[MAXN + 1];
int top = 0;
for (int i = 0; i < n; i++) {
node *p = &T[i];
while (top && S[top]->val < p->val)
①;
if (top)
②;
S[++top] = p;
}
root = S[1];
}
void DFS(node *p) { // 构建 Euler 序列
A[p->dfn = t++] = p;
for (int i = 0; i < 2; i++)
if (p->son[i]) {
p->son[i]->dep = p->dep + 1;
DFS(p->son[i]);
A[t++] = p;
}
p->end = t - 1;
}
node *min(node *x, node *y) {
return ③ ? x : y;
}
void ST_init() {
b = (int)(ceil(log2(t) / 2));
c = t / b;
Log2[1] = 0;
for (int i = 2; i <= c; i++)
Log2[i] = Log2[i >> 1] + 1;
for (int i = 0; i < c; i++) {
Min[0][i] = A[i * b];
for (int j = 1; j < b; j++)
Min[0][i] = min(Min[0][i], A[i * b + j]);
}
for (int i = 1, l = 2; l <= c; i++, l <<= 1)
for (int j = 0; j + l <= c; j++)
Min[i][j] = min(Min[i - 1][j], Min[i - 1][j + (l >>1)]);
}
void small_init() { // 块内预处理
for (int i = 0; i <= c; i++)
for (int j = 1; j < b && i * b + j < t; j++)
if (④)
Dif[i] |= 1 << (j - 1);
for (int S = 0; S < (1 << (b - 1)); S++) {
int mx = 0, v = 0;
for (int i = 1; i < b; i++) {
⑤;
if (v < mx) {
mx = v;
Pos[S] = i;
}
}
}
}
node *ST_query(int l, int r) {
int g = Log2[r - l + 1];
return min(Min[g][l], Min[g][r - (1 << g) + 1]);
}
node *small_query(int l, int r) { // 块内查询
int p = l / b;
int S = ⑥;
return A[l + Pos[S]];
}
node *query(int l, int r) {
if (l > r)
return query(r, l);
int pl = l / b, pr = r / b;
if (pl == pr) {
return small_query(l, r);
} else {
node *s = min(small_query(l, pl * b + b - 1),small_query(pr * b, r));
if (pl + 1 <= pr - 1)
s = min(s, ST_query(pl + 1, pr - 1));
return s;
}
}
int main() {
int m;
cin >> n >> m;
for (int i = 0; i < n; i++)
cin >> T[i].val;
build();
DFS(root);
ST_init();
small_init();
while (m--) {
int l, r;
cin >> l >> r;
cout << query(T[l].dfn, T[r].dfn)->val << endl;
}
return 0;
}
|
38、①处应填( )
A. p->son[0] = S[top–]
B. p->son[1] = S[top–]
C. S[top–]->son[0] = p
D. S[top–]->son[1] = p
【参考答案】A
39、②处应填( )
A. p->son[0] = S[top]
B. p->son[1] = S[top]
C. S[top]->son[0] = p
D. S[top]->son[1] = p
【参考答案】D
40、③处应填( )
A. x->dep < y->dep
B. x < y
C. x->dep > y->dep
D. x->val < y->val
【参考答案】A
41、④处应填( )
A. A[i * b + j - 1] == A[i * b + j]->son[0]
B. A[i * b + j]->val < A[i * b + j - 1]->val
C. A[i * b + j] == A[i * b + j - 1]->son[1]
D. A[i * b + j]->dep < A[i * b + j - 1]->dep
【参考答案】D
42、⑤处应填( )
A. v += (S » i & 1) ? -1 : 1
B. v += (S » i & 1) ? 1 : -1
C. v += (S » (i - 1) & 1) ? 1 : -1
D. v += (S » (i - 1) & 1) ? -1 : 1
【参考答案】D
43、⑥处应填( )
A. (Dif[p] » (r - p * b)) & ((1 « (r - l)) - 1)
B. Dif[p]
C. (Dif[p] » (l - p * b)) & ((1 « (r - l)) - 1)
D. (Dif[p] » ((p + 1) * b - r)) & ((1 « (r - l + 1)) - 1)
【参考答案】C


